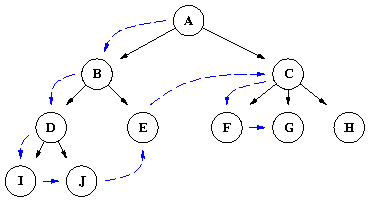
Depth First Search
The algorithm we chose to use for our robot is the depth-first search. In depth-first search, we search a tree structure by going down to the lowest leaf node, then it traverses back up the tree to look for the next unexplored node.
Source of image
We chose this algorithm because our nodes, which reperesent grid squares in the maze, are adjacent to each other on the tree, so using a depth-first search would be most efficient in order to prevent doing unnecessary traveling. In addition, depth-first search has lower memory requirements than breadth-first search, making it very ideal for a limited-memory microprocessor like the Arduino.
Implementing the Tree
To implement our tree structure for the maze, we created the class Node. Node will represent each square of the grid. This structure will keep track of all the coordinate, wall, and treasure info for that particular grid space. It also keeps track of the grid's neighbors, and where the robot has come from to reach that grid space (parent Node). Below is our Node header file.
class Node {
int dir;
char coord; //0-19
//NSEWTT0F: NSEW = walls, TT = treasure, F = flag for done exploring
char wallTreasures;
Node* neighbors[3]; //pointer to neighboring nodes
Node* parent; //pointer to parent node
int nextNeighbor;
public:
Node(int);
void addNeighbor(Node*);
void addWall(Direction, bool);
bool isExplored();
void addTreasure(int freq);
void addParent(Node*);
void markAsExplored();
Node** getNeighbors();
Node* getParent();
char getCoord();
char getWallTreasures();
int neighborCoord(Direction facing, int sensor, int currPos);
};
Using these classes, in the video above when the robot detects an intersection, we output the robot's current position, current direction, any walls detected, and the next position we travel to. When the robot reaches the final node, it prints a done text.
There are a few difficulties in representing a maze as a tree. The biggest problem is that our maze "tree" isn't necessarily a tree, it could be a graph. This means that if we have 4 grids arranged in a square, there is a possibility that our robot would be stuck in that loop and exploring those nodes over and over without ever moving on to a different node. This was taken care of using a flag bit in wallTreasures. When a Node has been expanded (meaning that we have looked at its walls and neighbors), this flag signals that the node has been fully explored. Next time, if we see this Node, we do not add it to the tree, and we do not explore it again.
Implementing the DFS
Now that we have set up our Node structure, we have to implement the DFS itself. This is actually done in another class we called Explorer, whose header file is shown here.
class Explorer {
Node* root;
Node* current;
public:
Explorer(Node* startNode);
Node* nextNode(); //essentially does the DFS
Node* travelTo(Node*); //call this when robot has moved
Node* getCurrNode(); //returns current node
bool isDone();
};
This class has all the logic for searching/processing. The tree needs only the information regarding the root Node, and the current Node the robot is at. It does not even need to save a "frontier" or array of nodes to explore, since it will simply traverse up and down the tree, based on whether the current Node has unexplored neighbors. In essence, we are saving only one node at all times!! :D
To quickly note, the reason that the search algorithms have a frontier list is because the tree structures assumed there do not have a parent as we've specified in our Node class. With our structure, we are able to see what Nodes we are coming from by simply traversing back up the tree.
Robot Implementation
Now that we've discussed the classes we wrote that implement the tree and searching, we can finally talk about the big idea of how we're implementing our robot. (You're almost there, TAs!) The idea is that as our robot traverses the maze, it builds a tree using our Node class. We initialize all 20 Nodes in setup(), since our maze is a fixed size. As the robot explores, it builds the neighbor/parent connections as we've set up in our tree.
Simulation
Given the task of developing a maze exploration algorithm, it is inconvenient to have to go into lab and set up a maze for our robot any time we want to run tests. In this milestone, we built a simulation in Java to model the maze and the robot as it explores the maze. The user can track the location and direction of the robot as well as explored/unexplored portions of the maze through a graphic display. The simulator will also keep track of the number of visitable nodes still unvisited and print "Done!" to the console upon maze completion. Using the simulation, we can build and test algorithms on randomly generated mazes to determine the fitness of any algorithms we plan to use on our robot. Also, when implementing the algorithms in simulation, we can get a better idea for how much memory will be needed to implement it on Arduino.
In its current state, the simulator has limited functionality. We did not implement treasures in the maze and the mazes that are generated often have large unexplorable portions which may not be accurate to the actual competition. The current version does, however, support most of the essential components of maze exploration. We implemented two algorithms in simulation. The first we implemented was a random search. This algorithm can solve any maze, but it may require long periods of time to solve the maze completely. With this algorithm, the robot will often wander randomly through space it has already explored looking for unexplored spaces, making this algorithm non-ideal for the cometition. The second algorithm we implemented was a Depth First Search. This algorithm is much more efficient that random exploration because the robot builds a tree to represent the maze as it explores. There still exist some bugs in our DFS which were found through testing, one of which causes the robot to get stuck in the maze after reaching a dead end. Despite the bugs, we were able to get a good feel for how well DFS works in mazes. While it performs much better than random search, DFS does have drawbacks in that it builds trees and cannot make a graph with cycles. This leads to the robot backtracking through explored spaces rather than taking the most direct route to unexplored spaces. The performance of our algorithms can be seen in the video posted above.
The simulator has allowed us to run many test on our current algorithm, allowing us to find areas to improve performance. For example, our current DFS requires the robot to return to the start node to detect that it has finished exploring. For the final cometition, changing our finish condition will certainly save us a fair amount of time. One of the emphasis for the simulator is user friendliness. Testing out an exploration algorithms only requires changing one method in the Robot class and accessing sensor values in that class. Almost no knowledge of the simulator framework is needed to write and test an algorithm. For this reason, we encourage future 3400 students to download and use our simulator which is available here